Trabajo en clase N°3

Actividad en clase: campos vectoriales

https://1drv.ms/b/s!AjkugOysC0vzgjd7lmD3dvH5YpY5

Trabajo en clase N°2

Actividad en clase: 2016- julio-21

https://1drv.ms/b/s!AjkugOysC0vzgjyhegi7LPM5mVJe

Deber N°15

Conservación de la energía

https://1drv.ms/b/s!AjkugOysC0vzgjja27PdgSKH-ng4

Deber N°14

Integral de línea

https://1drv.ms/b/s!AjkugOysC0vzgj_BPZmdROKXjfBK

Deber N°13

Campos vectoriales

https://1drv.ms/b/s!AjkugOysC0vzgjsXFqnTA6zC9RSA

Deber N°12

Integrales Múltiples

https://1drv.ms/b/s!AjkugOysC0vzghuC-pAUhNT6pIkN

Deber N°11

Integrales múltiples

https://1drv.ms/b/s!AjkugOysC0vzgioFCbCLOKvPwvzb

Corrección II Bimestre

Prueba N°1
https://1drv.ms/b/s!AjkugOysC0vzgjnq8284uXypS2Bu

Deber N°10

Máximos y mínimos

https://1drv.ms/b/s!AjkugOysC0vzghjawX5cU7aazoPG

Deber N°9

Aproximaciones lineales

https://1drv.ms/b/s!AjkugOysC0vzghU_JEGAJXBkbs5c

Deber N°8

Derivadas direccionales

https://1drv.ms/b/s!AjkugOysC0vzgidrFzhupg7NEx1E

Clase N°27

2016-agosto-9

Teorema de Green

Sea C una curva simple, cerrada, uniforme por segmentos con orientación positiva en el plano, y sea D la región que delimita C. Si P y Q tienen derivadas parciales continuas en una región abierta que contiene a D, entonces:

Referencias:

Cálculo de varias variables. Sección 16.4
https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view

Deber N°7

Derivadas parciales

https://1drv.ms/b/s!AjkugOysC0vzgiQYuedfVnbVJQ--

Deber N°6

Funciones de varias variables

https://1drv.ms/b/s!AjkugOysC0vzgiGFEh1PVptC57cX

Límites y continuidad

https://1drv.ms/b/s!AjkugOysC0vzgiADAT9jiyhArtvP

Clase N°26

2016-agosto-4

Conservación de la energía

En un campo de fuerzas continuo F se hace que se desplace un objeto a lo largo de una trayectoria C definida por ,r(a)=  A , donde es el punto inicial y es el punto final de C. De acuerdo con la segunda ley de Newton del movimiento, la fuerza Frt en un punto sobre C se relaciona con la aceleración mediante la ecuación:

F(r(t))=  mr"(t)


Si un objeto se mueve desde un punto A hacia otro punto B bajo la influencia de un campo de fuerzas conservativo, entonces la suma de su energía potencial y de su energía cinética es constante. Este enunciado recibe el nombre de ley de la conservación de la energía, y es la razón de que el campo vectorial se llame conservativo.


Referencias:

Cálculo de varias variables. Sección 16.3
https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view

Clase N°25

2016-agosto-2

Integral de línea

Teorema fundamental de integrales de linea

P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz

Diferencial exacta

Si es exacta sus derivadas parciales son continuas y por lo tanto es conservativa. Existe una función
f(x,y,z)=P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz  tal que:

Clase N°24

2016-julio-28

Divergencia & Rotacional de Campos Vectoriales

DIVERGENCIA (div V)

Sea V(x,y,z) un campo vectorial su divergencia esta definida por:

ROTACIONAL (Rot B)

Sea B(x,y,z) un campo vectorial su rotacional esta definido por:



Observación:
Si F es un campo vectorial definido en el espacio cuyas derivadas parciales son continuas y Rot F=0, entonces F es un campo vectorial conservativo

Integral de Línea

Referencias:

Integrales de línea. Recuperado de: http://www.wikimatematica.org/index.phptitle=Integrales_de_l%C3%ADnea  Fecha:2016-julio-28

Clase N°23

2016-julio-26

Campos Vectoriales

Un campo vectorial se define como una función que se define sobre un vector en Rn, es decir, un vector que se transforma en otro vector gracias a una función f:

Ejemplos:

Trabajo en clase N°1

Actividad en clase: 2016-julio-7

https://1drv.ms/b/s!AjkugOysC0vzgjpw_4_HzZoPGeXz

Clase N°22

2016-julio-21

Aplicaciones de las integrales múltiples

Masa

    

*Distribución lineal de masa: cuando tiene una sola dimensión

*Distribución superficial de masa: cuando el cuerpo tiene 2 dimensiones

*Distribución volumétrica de masa: cuando el cuerpo tiene 3 dimensiones

Momentos de inercia

Centro de masa

*El centro de masa de una figura plana se define como las coordenadas de un cuerpo en el cual se encuentra concentrada toda la masa.

Referencias:
Cálculo de varias variables. Sección 15.5
https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view
CISNEROS "INTEGRALES MULTIPLES Y SUS APLICACIONES"

Clase N°21

2016-julio-12

Propiedades de la integral doble

i) Linealidad
ii) Asociativa
iii) Aditividad
iv) Comparación

 

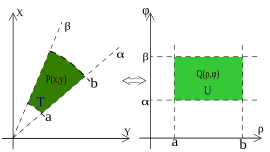
Transformaciones de integrales múltiples

Se realiza la transformación cuando se esta trabajando en un área que no es rectangular, de esta manera se facilita la resolución de la integral múltiple.

Esta transformación se logra con la ayuda del Jacobiano (J).

• Coordenadas polares

   y= rsenΘ                     x= rcosΘ

• Coordenadas cilíndricas

  y= rsenΘ                   x= rcosΘ                     z=z

• Coordenadas esféricas

  y= ᴩsenΘsenΦ          x=ᴩcosΘsenΦ            z=ᴩcosΦ

Referencias:
LARA J. Y GALINDO E., “INTRODUCCION AL CALCULO VECTORIAL”, Quito; 2009
Cálculo de varias variables. Sección 15.9
https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view

Clase N°20

2016-julio-7

Integrales Múltiples

Definición:

 

Al subdividir en rectángulos más pequeños se puede definir como:

* Se dice que f(x,y) es integrable si el límite existe.

* Las funciones continuas son integrables. 

Tipos de regiones

• Regiones rectangulares

R={(x,y)∈R^2  /a≤y≤b;c≤x≤d}

 

• Regiones entre curvas de tipo 1

• Regiones entre curvas de tipo 2

  

Referencias:

Galindo,Edwin. Calculo Vectorial. Prociencia Editores, Ecuador, 2009.
Cálculo de varias variables. Sección 15.5
https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view

Clase N°19

2016-julio-5

Máximos y Mínimos

*Máximos ^ Mínimos absolutos

*Máximos ^ Mínimos condicionados

*Multiplicadores de Lagrange

En los problemas de optimización, el método de los multiplicadores de Lagrange, llamados así en honor a Joseph Louis Lagrange, es un procedimiento para encontrar los máximos y mínimos de funciones de múltiples variables sujetas a restricciones. Este método reduce el problema restringido con n variables a uno sin restricciones de n + k variables, donde k es igual al número de restricciones, y cuyas ecuaciones pueden ser resueltas más fácilmente. Estas nuevas variables escalares desconocidas, una para cada restricción, son llamadas multiplicadores de Lagrange. El método dice que los puntos donde la función tiene un extremo condicionado con k restricciones, están entre los puntos estacionarios de una nueva función sin restricciones construida como una combinación lineal de la función y las funciones implicadas en las restricciones, cuyos coeficientes son los multiplicadores.

Referencias:

Cálculo de varias variables. Sección 14.7

https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view

Clase N°18

2016-junio-30

Máximos y mínimos

*Máximos o mínimos relativos

Definición:

TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
Sea f una función dos veces derivable en un intervalo abierto I, sea c un punto de I,
tal que f '(c) = 0 . Entonces:
i. Si f ' '(c) < 0 , entonces, f presenta un máximo relativo en c.
ii. Si f ' '(c) > 0 , entonces, f presenta un mínimo relativo en c.


Para el caso de los absolutos
1) puntos estacionarios, primera derivada se reemplaza en z
2) puntos de fronteras
3) puntos de los vértices

Referencias:

Cálculo de varias variables. Sección 14.7

https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view

Clase N°17

2016-junio-28

Regla de la Cadena

Recordemos que la regla de la cadena para una función y = f(x) ; y x = g(t,), ambas funciones derivable, entonces y es una función derivable con respecto a t .

Para funciones de varias variables, la regla de la cadena tiene varias versiones.

Ejemplo:

Clase N°16

2016-junio-23

Aproximaciones lineales

TEOREMA

Ejercicio

Referencias:

Cálculo de varias variables. Sección 14.4

https://drive.google.com/file/d/0B3NNTBVL1_YVZDR4ZUN5OEl6REU/view